문제

트리가 주어지고, 이 트리를 각각 전위, 중위, 후위 순회 하는 문제였다.
트리 구조를 만드는 것 자체는 쉽지만, 이 트리를 탐색하는 방법을 생각하는 것이 조금 어려웠던 문제였다.
나는 실제 그래프 모양대로 배열을 만들어가며 문제를 풀었다.
풀이
1. 전위 순회
전위 순회는 루트 -> 왼쪽 자식 -> 오른쪽 자식의 순서대로 순회하는 방법이다.
각 계층별로 루트를 먼저 돌기 때문에, 루트를 먼저 체크하고 왼쪽 루트로 내려간다.
다음 계층에서도 왼쪽 루트를 돌고, 만약 더이상 왼쪽 루트가 없다면 오른쪽 루트를 돈다.
오른쪽 루트도 없다면 다시 한층 위로 올라가 오른쪽 루트가 있는지 확인한다.
다시 A 노드로 돌아갔다면, 오른쪽 노드를 똑같은 방식으로 탐색하면 된다.

전위 순회는 깊이 우선 탐색, 즉 'DFS'와 똑같은 메커니즘을 가지고 있기 때문에, DFS와 같은 방식으로 풀어줬다.
const preorder = ["A"];
const preorderT = (cur) => {
if (!graph[cur]) return;
for (let next of graph[cur]) {
if (next !== ".") {
preorder.push(next);
preorderT(next);
}
}
};
preorderT("A");
2. 중위 순회
전위 순회는 왼쪽 자식 -> 루트 -> 오른쪽 자식의 순서대로 순회하는 방법이다.
쉽게 말해, 배열로 순서를 저장한다고 치면 [왼쪽, 루트, 오른쪽]의 순서대로 저장된다는 것이다.
그래서 나는 BFS를 사용해 A 노드부터 왼쪽-> 오른쪽 순서대로 탐색하며
왼쪽에 자식이 있다면 현재 노드의 왼쪽에, 오른쪽에 자식이 있다면 오른쪽에 자식을 붙여주는 방법을 사용했다.
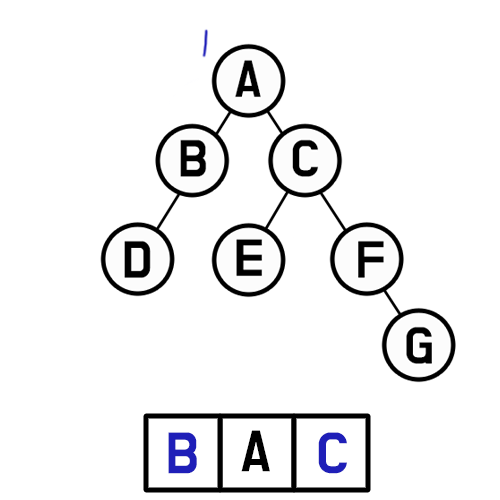
현재 탐색중인 노드는 A이고, 배열에도 A가 들어있다.
A의 자식 노드는 B, C이므로, A의 양옆에 B와 C를 붙여주고, 다음 탐색할 노드에 B와 C를 추가한다.
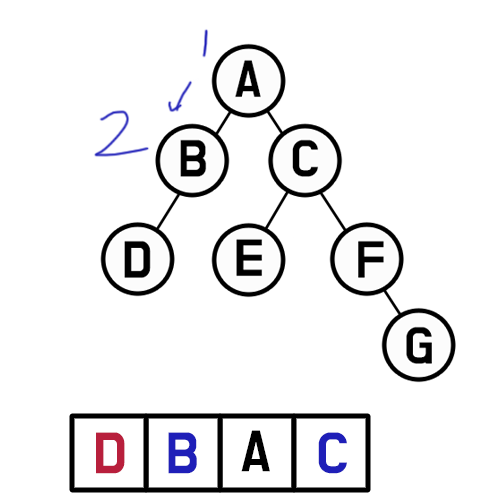
B를 탐색하면서 똑같이 자식 노드를 자신의 양옆에 붙여주고, 다음 탐색할 노드에 추가해 준다.
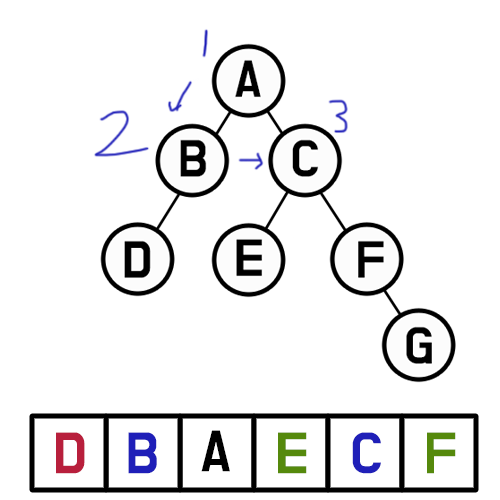
C를 탐색하며 C의 자식 노드인 E와 F를 C 양 옆에 붙여주고, 역시 큐에 추가해 준다.

D와 E는 자식 노드가 없으므로 패스하고, 마지막 F의 자식 노드는 오른쪽 자식인 G뿐이므로, G를 F의 오른쪽에 넣어 준다.
G도 자식이 없으므로 반복은 여기서 종료된다.
이런 식으로 현재 탐색하는 노드의 왼쪽, 오른쪽에 각각 자식 노드들을 붙여 주면 중위 순회 노드의 탐색 순서를 구할 수 있다.
양옆에 넣어주는 방법은 현재 탐색중인 노드의 인덱스를 구한 뒤, 해당 인덱스의 바로 앞, 뒤를 자른 다음 자식 노드를 넣고 다시 합쳐주는 방식을 택했다.
원시적이지만 이 방법밖에 생각이 나지 않았다wwww
그래서 순서를 담는 배열이 const가 아니라 let이다.
let inorder = ["A"];
const inorderT = (start) => {
const queue = [start];
while (queue.length > 0) {
const cur = queue.shift();
if (!graph[cur]) continue;
for (let i = 0; i < 2; i++) {
const next = graph[cur][i];
const idx = inorder.indexOf(cur);
if (next !== ".") {
if (i === 0) {
inorder = [...inorder.slice(0, idx), next, ...inorder.slice(idx)];
} else {
inorder = [
...inorder.slice(0, idx + 1),
next,
...inorder.slice(idx + 1),
];
}
queue.push(next);
}
}
}
};
inorderT("A");
3. 후위 순회
후위 순회는 왼쪽 자식 -> 오른쪽 자식 -> 루트 순으로 순회하는 방법이다.
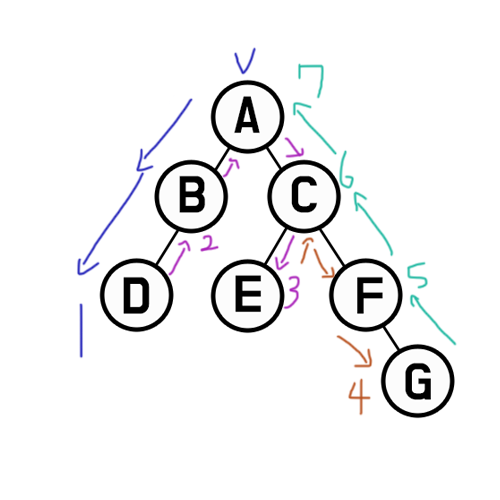
루트를 맨 나중에 찍기 때문에, 가장 아래쪽의 자식까지 내려간 후 역순으로 탐색하는 것과 같다.
자세히 보면, 1~7까지가 아닌 7~1까지 거꾸로 봤을 때,
A 노드부터 오른쪽 노드 순서대로 내려가면서 숫자가 줄어드는 것을 볼 수 있다.
나는 이것을 '좌우가 뒤집힌 역방향 DFS'라고 생각해서, DFS 방식으로 풀되, 탐색 순서와 배열에 넣는 순서를 완전히 거꾸로 해서 해결 할 수 있었다.
쉽게 말해, 좌->우 순서 탐색이 아니라 우-> 좌 순서대로 넣었고, 현재 탐색하는 노드를 배열의 맨 뒤에 넣는것이 아니라 맨 앞에 넣는 방식을 택했다.
사실, 맨 뒤에 넣고 reverse()를 해도 되긴 한다. unshift보단 push의 시간 복잡도가 더 낮기 때문에 훨씬 효율적인 방법이기도 하다.
이걸 문제 다 풀고 글을 쓰면서 생각이 났다는 것이지 문제지만,..,.,
const postorder = ["A"];
const postorderT = (cur) => {
if (!graph[cur]) return;
for (let i = 1; i >= 0; i--) {
const next = graph[cur][i];
if (next !== ".") {
postorder.unshift(next);
postorderT(next);
}
}
};
postorderT("A");
코드
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const input = [];
rl.on("line", (line) => {
input.push(line.split(" "));
}).on("close", () => {
const [n] = input.shift();
const graph = {};
for (let route of input) {
const [start, ...routes] = route;
graph[start] = [];
for (end of routes) {
graph[start].push(end);
}
}
const preorder = ["A"];
const preorderT = (cur) => {
if (!graph[cur]) return;
for (let next of graph[cur]) {
if (next !== ".") {
preorder.push(next);
preorderT(next);
}
}
};
preorderT("A");
let inorder = ["A"];
const inorderT = (start) => {
const queue = [start];
while (queue.length > 0) {
const cur = queue.shift();
if (!graph[cur]) continue;
for (let i = 0; i < 2; i++) {
const next = graph[cur][i];
const idx = inorder.indexOf(cur);
if (next !== ".") {
if (i === 0) {
inorder = [...inorder.slice(0, idx), next, ...inorder.slice(idx)];
} else {
inorder = [
...inorder.slice(0, idx + 1),
next,
...inorder.slice(idx + 1),
];
}
queue.push(next);
}
}
}
};
inorderT("A");
const postorder = ["A"];
const postorderT = (cur) => {
if (!graph[cur]) return;
for (let i = 1; i >= 0; i--) {
const next = graph[cur][i];
if (next !== ".") {
postorder.unshift(next);
postorderT(next);
}
}
};
postorderT("A");
const ans = [preorder.join(""), inorder.join(""), postorder.join("")];
console.log(ans.join("\n"));
process.exit(0);
});
예제와 반례는 다 맞는데 계속 문제가 틀려서 확인헤 보니 input 단계에서 split()을 하지 않고 그냥 통 문자열을 집어넣어 발생한 오류였다.
이걸로 30분 넘게 헤멘 내가 레전드레전드
'코딩 테스트 풀이 > 백준' 카테고리의 다른 글
| [C4] 11725 - 트리의 부모찾기 (0) | 2024.12.06 |
|---|---|
| [C3] 5430 - AC (0) | 2024.12.04 |
| [C4] 1149 - RGB거리 (3) | 2024.11.28 |
| [C3] 1260 - DFS와 BFS (0) | 2024.11.27 |
| [C3] 9375 - 패션왕 신해빈 (0) | 2024.11.25 |



